みんなの周りには、まん丸い形のものがたくさんあるよね。お皿、コップの口、ボール、時計の文字盤、自転車のタイヤ…。大きさは違うけれど、どれもきれいな「円」の形をしている。
今日は、この「円」が持っている、ちょっと不思議でとても大切な「数字の秘密」についてお話ししよう。その秘密の名前は「円周率」。聞いたことないかな?大丈夫、この記事を読めば、君も円周率博士になれるはず!

はると
うわっ、「円周率」か〜!名前からして難しそうだな…。俺、数字って苦手なんだよな。ボールみたいに丸いのは好きだけど!⚽

ひまり
もう、はるとったら。食わず嫌いはダメよ。この記事、身近な「まる」から説明してくれてるみたいだし、きっとはるとでも分かるって!私が隣で見ててあげるから♪
まるの「ぐるりの長さ」と「まっすぐな線の長さ」の関係
まず、「円」の基本的な部分の名前を確認しよう。
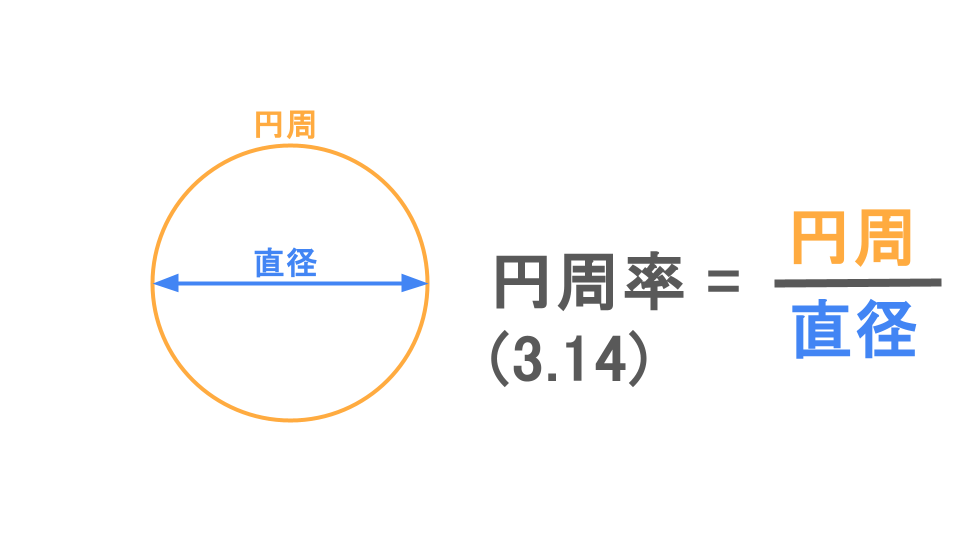
- 円周:円の「まわりの長さ」、ぐるっと一周した長さのことだよ。メジャーやヒモを使って測れるね。
- 直径:円の中心を通って、円の端から端までまっすぐに引いた線の長さのこと。円をちょうど半分こにする線だね。定規で測れるよ。
さて、ここからが本題。どんな大きさの円でも、例えば、お菓子の缶のような小さな円でも、運動場の真ん中に描かれた大きな円でも、その「円周」の長さを「直径」の長さで割ってみると、いつもほぼ同じ値になるんだ!
びっくりだよね?
円周÷直径=いつもだいたい同じ数
この「いつもだいたい同じ数」こそが、円周率なんだ。

円周率って、いくつなの?
じゃあ、その「いつもだいたい同じ数」って、具体的にどれくらいなんだろう?
みんなが学校で習うのは、たぶん「およそ3.14」という値だと思う。
実際に、身の回りの丸いもので試してみると面白いよ。
やってみよう!身近な「まる」で円周率を確かめる
- 丸いものを探す:お皿、CDやDVD、ペットボトルの底、フタなど、きれいな円の形をしたものをいくつか見つけてみよう。
- 直径を測る:定規を使って、円の中心を通るように、端から端までの長さ(直径)を測る。できるだけ正確にね。センチメートル(cm)という単位で測ってみよう。
- 円周を測る:円のまわりの長さ(円周)を測る。これは定規だと難しいから、柔らかいメジャーを使うか、円のまわりにヒモをぴったり合わせて、そのヒモの長さを定規で測るといいよ。
- 割り算をする:測った「円周」の長さを、測った「直径」の長さで割ってみよう。(円周÷直径)
例えば、直径が7cmのお皿があったとして、メジャーで円周を測ったら約22cmだったとするね。
22÷7=3.14…
ほら!約3.14になったでしょ?
どうかな?ピッタリ3.14にはならないかもしれない。測り方によって少しズレちゃう(例えば、3.1とか3.2とか)こともあるけれど、どれも大体「3よりちょっと大きい」数になったんじゃないかな?
昔の人たちも、こうやって実際に測ってみて、「どんな円でも、円周は直径の約3倍ちょっとだな」ということに気づいたんだ。

円周率の使い方
円周率を知っていると、円に関する色々な計算ができるようになるよ。
1.円周の長さを計算する
直径がわかっていれば、円周率を使って円周の長さを計算できる。
円周=直径×円周率(3.14)
たとえば、直径10センチの円の円周は?
10×3.14=31.4センチ
2.円の面積を計算する
円の面積を計算するには、「半径」という、円の中心から縁までの長さを使うよ。半径は直径の半分だね。
円の面積=半径×半径×円周率(3.14)
たとえば、半径5センチの円の面積は?
5×5×3.14=78.5平方センチメートル
これで、丸いピザの大きさを計算したり、円形の公園の広さを求めたりできるね!
終わりがない!?円周率のふしぎな性質
さっき、「円周率はおよそ3.14」って言ったけど、実はこれ、「およそ」なんだ。本当の円周率は、3.14でぴったり終わりじゃない。
本当の円周率は…
3.14159265358979323846264338327950288419716939937510…
と、ずーっと、どこまでもどこまでも続くんだ!しかも、ただ続くだけじゃなくて、数字の並び方に決まったパターン(繰り返し)がないこともわかっている。「121212…」みたいに同じパターンが繰り返されることもないし、「5」が出たらずっと5が続くわけでもない。次に何の数字が出てくるか、予測できないんだ。
こういう「割り切れなくて、循環(同じ繰り返し)もしない小数」のことを、ちょっと難しい言葉で「無理数」って呼ぶよ。
なんだか不思議だよね。円という、とってもシンプルできれいな形から、こんなに複雑で、どこまでも続く数字が生まれてくるなんて!

円周率クイズ
ここで、ちょっと円周率に関するクイズをしてみよう!
問題1:直径が14cmの円の円周は約何cmでしょう?
(ヒント:円周=直径×円周率)
問題2:半径が10cmの円の面積は約何平方センチメートルでしょう?
(ヒント:円の面積=半径×半径×円周率)
問題3:円周率の小数点以下3桁目は何でしょう?
(ヒント:円周率は3.14159…)
答えは記事の最後に書いておくね。考えてみてください!
世界中の人たちが挑戦中!円周率の計算
この「終わりなき数字」円周率を、もっともっと詳しく知りたい!と、世界中の数学者やコンピュータ科学者たちが、スーパーコンピュータを使って計算を続けているんだ。
どれくらい計算されているかというと、なんと、もう100兆桁を超えているんだって!(2023年時点の情報だよ。もしかしたら君がこれを読んでいる時には、もっと記録が伸びているかも!)
100兆桁って、想像できる?もし1秒に1つの数字を読み上げるとしても、全部読み終わるのに300万年以上かかっちゃうくらい、とてつもない長さなんだ。
もちろん、普段の計算でそんなに長い桁数を使うことはないよ。学校のテストや、身の回りの簡単な計算なら「3.14」で十分なことが多い。もっと正確さが必要な科学技術の計算でも、せいぜい数十桁もあれば足りることがほとんどなんだって。
じゃあ、なぜそんなに計算するんだろう?それは、円周率の性質をもっと深く理解したいという好奇心や、コンピュータの性能を試すためでもあるんだ。

円周率の歴史–昔の人はどうやって計算したの?
円周率は、とっても昔から人々が関心を持っていた数なんだ。約4000年前の古代エジプトやバビロニアの時代から、人々は円周率の値を求めようとしていたんだよ。
古代エジプトでは、円周率を約3.16と考えていたという記録があるんだ。これは今の値(3.14159…)と比べるとちょっと大きいけど、当時としてはすごく良い近似値だったんだよ。
古代ギリシャの数学者アルキメデスは、円に内接する多角形と外接する多角形を使って、円周率が3.1408と3.1429の間にあると計算したんだ。これは今の値にすごく近いよね。
中国では、祖沖之という人が、5世紀頃に円周率が「3.1415926と3.1415927の間にある」と計算したと言われているよ。手計算でこんなに正確に求めるなんて、すごいよね!
今では、スーパーコンピュータを使って何兆桁も計算できるようになったけど、昔の人たちは本当に頭がよくて、工夫をこらして円周率に挑戦していたんだね。

はると
えっ!?円周率って3.14で終わりじゃないの!?100兆桁!?読むのに300万年!?俺、給食のカレーライス、5分で食べ終わるのに!🍛それより長いじゃん!

ひまり
ちょっとはると、早食い自慢しないの!ちゃんと噛んで食べなさいっていつも言ってるでしょ。…でも、昔の人がコンピュータなしで計算したってすごいわよね。アルキメデスとか祖沖之とか…歴史の部分、私ちょっと感動しちゃった。
円周率は何の役に立つの?
「ふーん、面白い数字なのはわかったけど、それって何の役に立つの?」って思うかもしれないね。円周率は、実は私たちの生活のいろいろな場面で、陰ながら大活躍しているんだよ。
1.円の周りの長さや面積を計算する
これが一番わかりやすい使い道だね。先ほど説明したように、円周や円の面積を計算するのに使われるよ。
例えば:
- 自転車のタイヤが1回転したらどれくらい進むかを計算するとき
- 丸いケーキを何等分かにしたときの、一人分の面積を計算するとき
- 円形の公園や花壇の周りにフェンスを設置するのに、どれくらいの長さが必要かを計算するとき
2.設計や科学技術で大活躍
円や球(ボールのような立体)の形は、自然界にも、人間が作るものにもたくさんある。
- ものづくり:車のタイヤ、エンジンの中の部品、CDやDVD、建物の柱、ドーム型のスタジアムなど、丸い形やカーブした形を設計するときには、円周率を使った計算が欠かせない。例えば、東京ドームのような大きな屋根を設計するとき、どれだけの材料が必要か、どれくらいの重さになるかなどを計算するのに円周率が使われているよ。
- 科学:惑星の軌道を計算したり、波の動きを分析したり、電気の流れを考えたり…実は物理学や工学のいろいろな場面で、円周率が登場するんだ。例えば、地球は太陽の周りをぐるぐる回っているけど、その軌道を計算するときに円周率が必要になるんだよ。
- コンピュータ:コンピュータグラフィックスでリアルな円を描いたり、ゲームの中で物が転がる動きを計算したりするのにも、円周率が使われているよ。君が好きなゲームの中で見る丸いものや、転がるボールの動きも、裏側では円周率を使って計算されているんだ。
3.意外なところでも活躍!
実は、音楽を聴くときや、デジタルカメラで写真を撮るときにも、円周率が関わっているんだよ。音や光の波の計算に円周率が使われているからなんだ。
また、お医者さんがCTスキャンという機械で体の中を調べるときにも、円周率を使った計算が行われているよ。
円周率のマーク「π」
ところで、円周率を表すときに、よく「π」という記号が使われるのを見たことがあるかな?これは「パイ」と読むギリシャ文字なんだ。
円周率が「π」と呼ばれるようになったのは、今から300年くらい前、1700年代にヨーロッパの数学者たちが使い始めて広まったと言われているよ。円周のことをギリシャ語で「ペリペトス」とか「ペリフェレイア」と言ったりするんだけど、その頭文字から取られた、という説があるよ。
いちいち「3.14159…」と書くのは大変だから、この記号「π」で円周率を表すのは、とても便利なんだ。
こんな公式を見たことがあるかな?
円周=2πr(rは半径)
円の面積=πr²(r²は「rの2乗」つまり「r×r」という意味)
算数の教科書にも出てくるよ。覚えておくと便利だね!
円周率を覚えよう!
円周率の値をたくさん覚えている人もいるんだよ。どうやって覚えるかというと、「語呂合わせ」という方法を使う人が多いんだ。
例えば、「さん、いち、し、いご、きゅう、に~」と円周率「3.1415926…」の数字を順番に日本語の言葉に当てはめて、覚えやすい文章を作るんだ。
「産医師異国に向こう(さんいしいこくにむこう)」(3.14159265…)
のように、数字を言葉に置き換えた文章を作って覚えるよ。
君も自分なりの語呂合わせを考えてみない?
まとめ:円周率は身近な「ふしぎ」への入り口
今日は、円周率について学んできたね。
- 円周率は、どんな円でも「円周÷直径」で求められる、特別な値のこと。
- およその値は「3.14」だけど、本当はどこまでも続く、終わりのない不思議な小数。
- 記号「π(パイ)」で表されることもある。
- 円の長さを計算したり、面積を求めたりするのに使われるだけでなく、科学技術のいろいろな場面で役立っている。
円周率は、算数や数学の世界にある、たくさんの面白い「ふしぎ」の入り口の一つ。身の回りの「まる」を見つけたら、「この円周は、直径の約3.14倍なんだな」と思い出してみてね。
これからも、身の回りの「なぜ?」「どうして?」を大切にして、いろいろなことを学んでいこう!算数や理科の世界には、円周率のように、知れば知るほど面白い発見がたくさん待っているよ!

はると
ふーん、円周率って「π」って書くんだな。…なぁ、ひまり、このマーク、なんか俺の嫌いなパクチー🌿に似てないか?見るだけで思い出して覚えにくいぞ…!

ひまり
もう、はるとったらパクチーのことばっかり!全然似てないわよ!でも、無理に覚えなくてもいいんじゃない?私は好きな「いちごパイ🍓」のパイって覚えることにするわ♪覚え方は人それぞれ、ってことよ!
クイズの答え
問題1の答え:約44cm(計算:14×3.14=43.96cm)
問題2の答え:約314平方センチメートル(計算:10×10×3.14=314平方cm)
問題3の答え:1(円周率は3.14159…だから、小数点以下3桁目は1)
どれくらい正解できたかな?全問正解した人はすごい!もし間違えても大丈夫、これからもっともっと円周率のことを勉強していこう!
楽天ブックス
¥345 (2026/02/08 21:24時点 | 楽天市場調べ)
 ポチップ
ポチップ